आकाशगंगा, चक्रीवादळ, पानं, शंखांमध्ये दिसणारी रुक्ष गणिताची फिबोनाची गंमत तर पाहा!

शाळेतले दिवस आठवतात का? भाषेच्या पुस्तकातल्या कविता, इतिहासातल्या मनोरंजक गोष्टी, भूगोलातले खारे वारे -मतलई वारे, विज्ञानातला न्यूटन, युरेका युरेका असं म्हणत रस्त्यावर धावणारा आर्किमीडीज, बेन्झिनच्या रेणूंचे स्वप्न बघणारा केक्युले, चित्रकलेच्या तासातले रंग.. सगळं काही आठवतं ना? पण गणित म्हटलं की बहुतेकांच्या कपाळाला आजही आठ्या पडतात. हा दोष बहुतेक गणित शिकवणार्या शिक्षकाचा असावा. कारण आयुष्यातल्या प्रत्येक घटनेशी गणिताचा कसा संबंध आहे हे त्यांनी आपल्याला शिकवलंच नाही. संख्या शिकवल्या, पण संख्यांचे स्वभाव शिकवले नाहीत.
आता एक सोपे उदाहरण बघा. आता ३१ डिसेंबरला तुम्ही चौपाटीवर फिरायला जाणार आहात. फिरायला निघताना मनात विचार येतो की आपण चौपाटीवर जातोय खरं, पण आपण जाऊ तेव्हा भरती असेल की ओहोटी? भरती असेल तर लाटांचा खेळ बघताना मज्जा येईल, पण ओहोटी असेल तर समुद्र पार मागे गेला असेल आणि सगळीकडे नुसता कचराच दिसेल. भरती की ओहोटी हे सांगण्यात तारीख फारशी मदत करणार नाही, पण त्या तारखेची तिथी कालनिर्णयवर बघा. त्या तिथीला ३/४ गुणा. जे उत्तर येईल तितक्या वाजता भरती असेलच. +
सांगायचा उद्देश हा की गणित हा कंटाळवाणा-रुक्ष विषय नसून अत्यंत मनोरंजक असा विषय आहे. फक्त मनोरंजकच नव्हे, तर निसर्गाच्या प्रत्येक अविष्कारासोबत तो जोडला गेला आहे. कसा? हे समजून घेण्याची आज एक खास संधी आहे. नुकताच फेबोनाची क्रम (फेबोनाची सिरीज) चा विशेष दिवस होता. हा कोण होता फेबोनाची? त्याचा क्रम काय होता आणि कसा निसर्गाशी तो जोडला गेला आहे हे वाचल्यावर तुम्ही नक्की विचाराल "असंही असतं गणितात "?
तर, साधारण ११७०मध्ये इटलीच्या पिसा गावात जन्मलेला लिओनार्डो फेबोनाची(Leonardo Fibonacci)हा एक गणिती होता. म्हणजे आताच्या काळात आपण त्याला गणिती म्हणतो. तो ज्या काळात जन्माला आला त्यावेळी शिकलेल्या माणसांना फक्त 'विद्वान' म्हणूनच संबोधीत केले जायचे.
तिसऱ्या शतकात आर्यभटाने शून्याची संकल्पना मांडली असली तरी तेराव्या शतकाच्या काळात युरोपात 'शून्य' ही संकल्पना पण पोहचली नव्हती. संख्या फक्त रोमन पध्दतीने लिहिल्या जायच्या. उदाहरणार्थ २०१३ हा आकडा (MMXIII) असा लिहीला जायचा. फेबोनाचीने त्याच्या पहिल्या पुस्तकात १ ते ९ आणि ० या आकड्यांची ओळख करून दिली. या पुस्तकाचे नाव होते Liber Abaci लिबेर अॅबासी. या पुस्तकात त्याचा उल्लेख फिलीयस बोनासी असा होता. त्याचा अर्थ बोनासीचा मुलगा असा लावला गेला आणि मुळात लिओनार्डो पिसानो नाव असलेल्या या अवलियाला जग लिओनार्डो फेबोनासी म्हणून ओळखायला लागले.
आज आपण ज्या फेबोनाची क्रमाची ओळख करून घेणार आहोत, त्या क्रमाला स्वतः फेबोनाचीने फारसे महत्व दिले नव्हते. त्याने या क्रमाला 'मनोरंजनात्मक गणित' म्हटले होते. पण नंतरच्या येणार्या काळात या क्रमाचा निसर्गाशी असलेला संबंध प्रस्थापित झाला तेव्हा या क्रमाचे महत्व जगाला कळले. हा संबंध नक्की कसा आपल्या रोजच्या आयुष्याशी जोडला गेला आहे हे बघण्यापूर्वी हा क्रम नक्की कसा आहे हे जाणून घेऊ या!
हा एक संख्यांचा संच किंवा क्रम आहे. या संचातील आकडे चढत्या क्रमाने मांडले तर येणारा पुढचा आकडा हा आधीच्या दोन आकड्यांच्या बेरजेइतका असतो. १, १, २, ३, ५, ८, १३, २१, ३४, ५५, ८९, १४४, २३३, ......... याला फेबोनाचीचा क्रम किंवा फेबोनाची सिरीज असे म्हणतात. या क्रमावर आधारित निसर्गाचे अनेक अविष्कार आपल्याला बघायला मिळतात. आपल्या झाडांवर येणार्या फांद्या, फुलांच्या पाकळ्या, फळातल्या बिया, समुद्राच्या भरतीत येणार्या लाटा, शेअरबाजारातील बदलणारे भाव या सगळ्यांना हा क्रम लागू पडतो. प्रश्न उरतो तो फक्त निरीक्षणाचा!!
हा क्रम शोधण्यासाठी फेबोनाचीने एक काल्पनिक उदाहरण घेतले होते. सशांची नुकतीच जन्माला अलेली एक नर-मादीची जोडी एक महिन्याची होते, तेव्हा ती प्रजनन करण्याच्या वयात आलेली असते. या जोडीने पुन्हा एकदा एक नर-मादीची जोडी जन्माला घातली तर दुसर्या महिन्यानंतर एकाच्या दोन जोड्या होतील, तिसर्या महिन्यानंतर आणखी एक जोडी जन्माला आल्यास एकूण जोड्या तीन होतील, त्या पुढच्या महिन्यात जोड्या पाच होतील. अशा पध्दतीने वर्षाच्या शेवटी २३३ जोड्या जन्माला आलेल्या असतील. अर्थात जन्माला आलेली जोडी मरण पावली नाही असं इथं गृहितक आहे.
आता निसर्ग म्हणजे विविधता आलीच नाही का? सशांच्या उदाहरणात आई-वडील अशी जोडी होती. पण वडील नाहीत, फक्त आईच एकटी पिल्लाला जन्म देते असं काही असलं तर? आता तुम्ही म्हणणार असं कधी असतंय का? असतं की हो राव!! मधमाशांच्या पोळ्यात राणी माशी फक्त जन्म देण्याचे काम करते. मादी माशीचा जन्म आई -वडील या जोडीतून होतो, तर नर माशीच्या जन्मासाठी फक्त मादी पुरेशी असते! आता विचारा फेबोनाचीला की बाबा तुझा क्रम इथे पण लागू होतो का? फेबोनाची म्हणतो इथे पण तेच तत्व लागू पडतं!
फक्त नर माशीच्या जन्मात क्रम असा असतो 1, 2, 3, 5, 8, .....
तर मादी माशीच्या जन्मात हा क्रम असा असतो. 2, 3, 5, 8, 13,
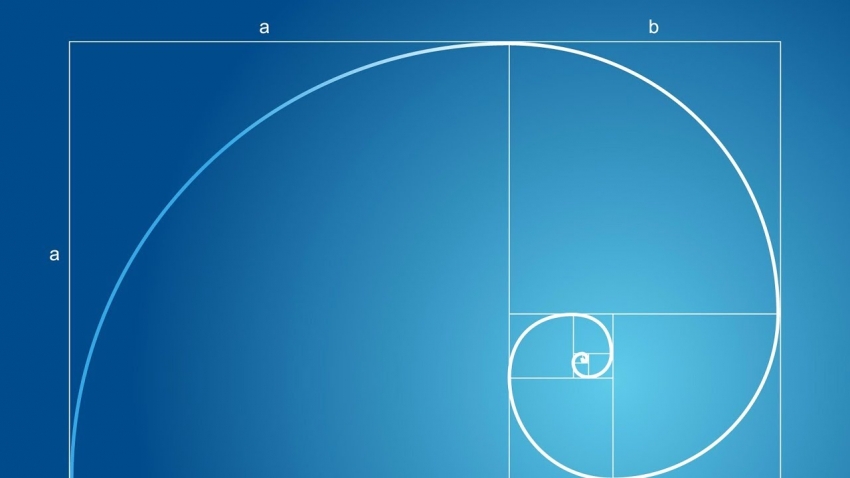
आता आपण बघू या हा फेबोनाचीचा क्रम निसर्गात कसा नजरेस येतो. ते पण त्यासाठी हा क्रम बहुमितीय आकृतीत कसा दिसेल यासाठी एक उदाहरण घेऊ या!
समजा, यासाठी फेबोनाचीच्या संख्याक्रमातल्या आकड्यांचे चौरस घेऊन त्यातून एक वक्राकृती त्यार केली, तर कशी दिसेल ते बघू या! नेमकी हीच वक्राकृती निसर्गात अनेक ठिकाणी बघायला मिळेल.
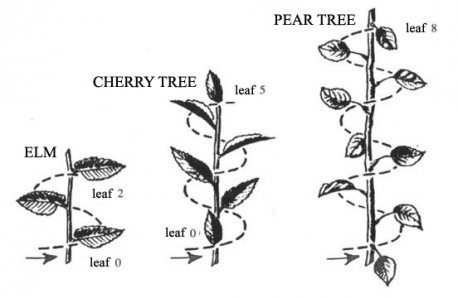
झाडावर येणारी पाने फेबोनाचीचा क्रम दर्शवतात हे दाखवणारे हे चित्र बघा . पहील्या पानानंतर दुसरे तीसतरे , किंवा पाचवे पान हे पुन्हा एकदा पहील्या पानासारखे येते .
बर्याचशा झाडांच्या फुलांच्या पाकळ्या ३,५,८, अशा संख्येत असतात.
एकाच ठिकाणी असलेला बियांचा संचय देखील फेबोनाचीच्या संख्यांची वक्राकृती दर्शवते.
मोठ्या वृक्षांच्या फांद्या पण फेबोनाचीच्या क्रमात येतात.
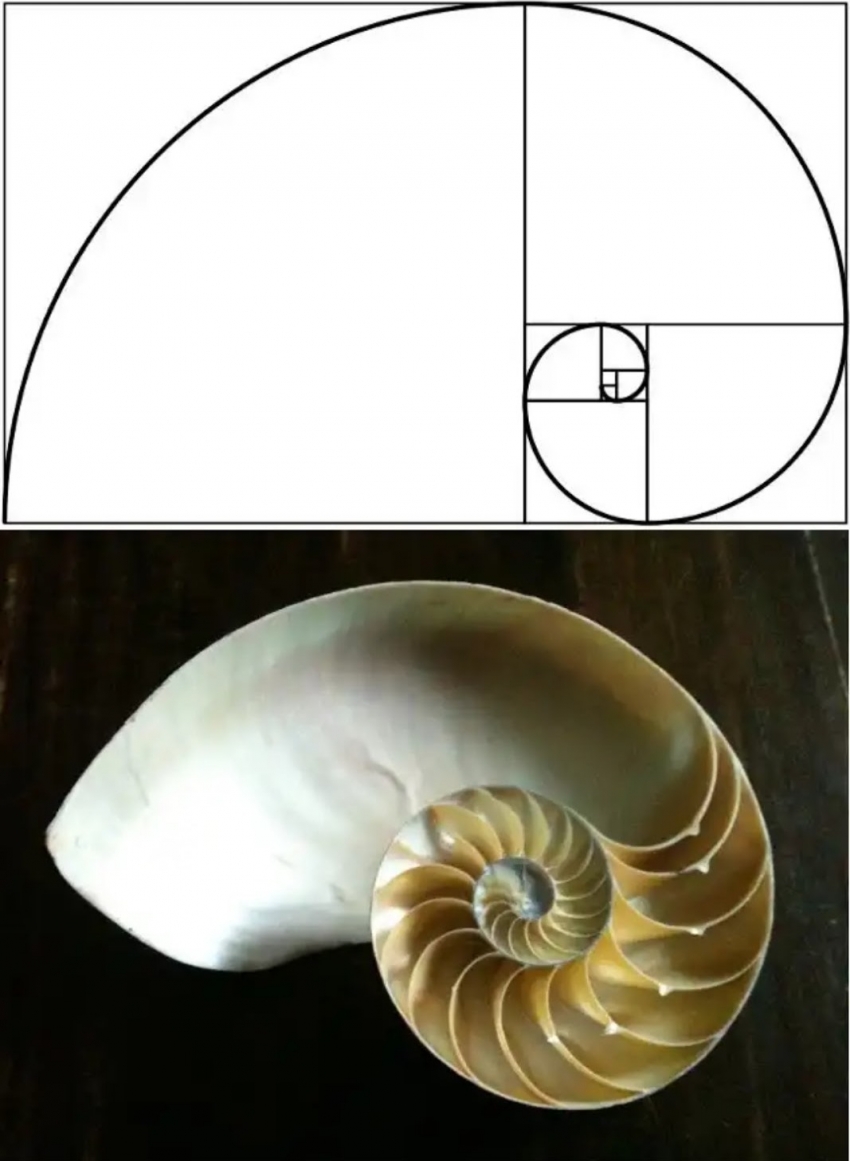
समुद्रात सापडणार्या शंख शिंपल्यात पण हाच क्रम दिसतो.
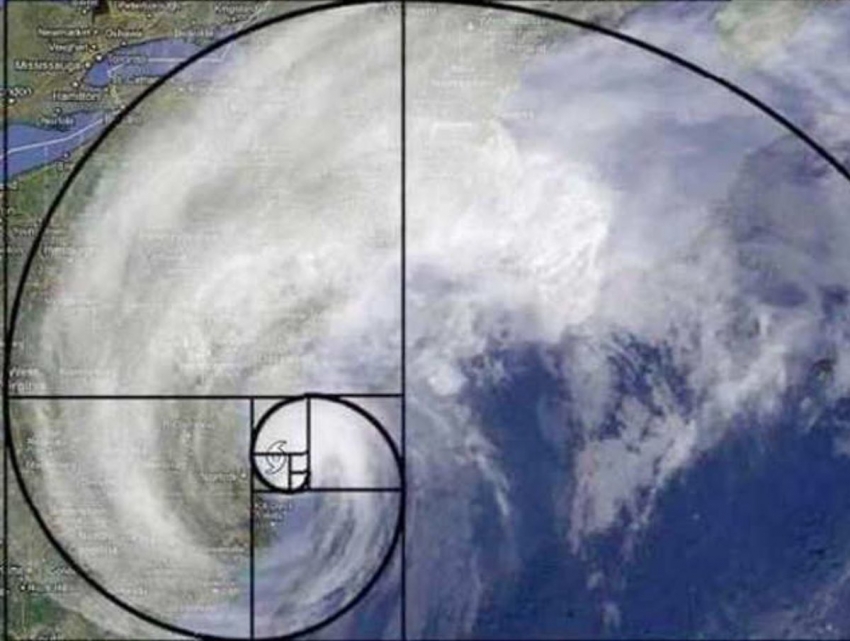
चक्रीवादळाच्या अनेक प्रतिमा तुम्ही बघीतल्या असतीलच , त्या प्रतिमेत पण हा क्रम स्पष्ट नजरेस येतो.
अवकाशातल्या अनेक अकाशगंगांच्या प्रतिमा पण या संच्याच्या आकृतीत बसतात.
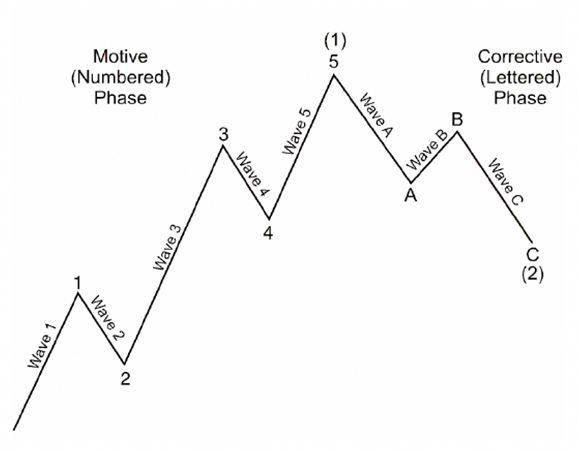
हे झाले निसर्गातले अनुभव पण शेअरबाजारात जे चढ उतार होतात त्याला पण फेबोनाचीचा क्रम लागू पडतो असे अनेकांचे म्हणणे आहे. या तज्ञांच्या मते शेअर बाजाराची हालचाल ग्राफच्या रुपात मांडली तर त्यात एकूण आठ लाटा असतात पहीली तेजीची लाट , दुसरी मंदीची , तीसरी पुन्हा तेजीची , तर चौथी मंदीची ! पाचवी तेजीची लाट शेवटची असते , त्यानंतर बाजार तीन लाटांअध्ये पडतो . पुन्हा एकदा एक ते आठ असा नवा क्रम चालू होतो. आजही बाजारातील अनेक व्यापारी थॉमस इलीयटने मांडलेल्या या वेव्ह थीअरीचा वापर करतात.
'दा विंची कोड' पुस्तक वाचलं असेल किंवा सिनेमा पाह्यला असेल, तर तिथेही तुम्ही हा उल्लेख पाह्यला असेलच. पण तेव्हा ते नेमकं काय आहे हे माहित नसेल. आता बिन्धास्त तुम्हीही तुमच्या मित्रांना फिबोनाची क्रमाबद्दल सांगा आणि कॉलर ताठ करा!!